John Mills
Doktoro, supera lekciisto en Universitato de Okcidenta Aŭstralio, Departemento de Elektra kaj Elektronika Inĝenierado, Nedlands WA 6009.
En novnaskitaj infanoj, precipe se ili antaŭtempe naskiĝis, iufoje la cerbon ne atingas sufiĉe da oksigeno. Eble parto de la pulmoj ne funkcias, aŭ eble la feta cirkulado de sango, en kiu la sango evitas la pulmojn, ankoraŭ iomete funkcias. Ĉiuokaze, oksigeno mankas en la sango, kaj tial ĝi mankas en la cerbo. Pro tio, eble la infano mortos, aŭ, pli tragedie, la cerbo nekuraceble difektiĝos.
La kuracado estas, ke la infano enspiru aeron, kiu enhavas pli da oksigeno ol la normala 21 %, eĉ ĝis 100 %. Tamen estas danĝero; se la infano enspirus tro da oksigeno, ĝi eble blindiĝus. Tial oni devas zorge regi la fluon de oksigeno, laŭ la bezono de la infano. Maŝino, kiu aŭtomate regus la oksigenon laŭ la bezono de la infano, plifaciligus la taskon de la kuracado, kaj, pli grave, pli bone traktus la infanon. Tiu ĉi artikolo priskribas la evoluadon de tia maŝino, kaj la problemojn de la projekto.
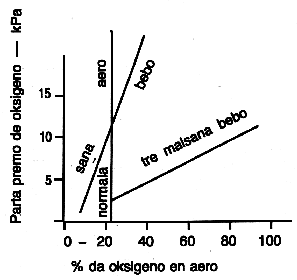
La cerbo ricevas oksigenon el la sango, kaj la difuzon de oksigeno en la cerbon regas la parta premo de oksigeno en la arteria sango, Pa O2. En sana infano tiu premo estas ĉirkaŭ 10,5 kPa. La cerbo ektuŝiĝus, se la premo iĝus malpli ol 8 kPa, kaj pro malpli ol 5,5 kPa la infano mortus. La oksigena premo rilatas al la proporcio de oksigeno en la aero, kiun la infano enspiras, Fi O2. Fig. 1 montras la rilaton.
 |  |
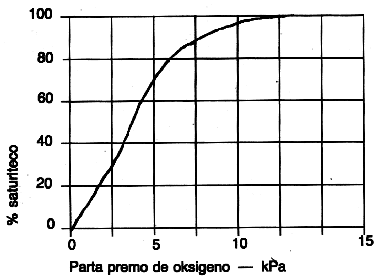
| Fig. 1: Oksigeno en la aero kaj en la sango | Fig. 2. Saturiteco per oksigeno kaj parta premo |
Por sana infano, la normala 21 % da oksigeno en la aero sufiĉas por premo ĝis pli ol 10,5 kPa en la sango, sed tre malsana infano bezonas eble 90 % da oksigeno (GUYTON 1976, SANO-KIKUCI 1985).
La oksigeno parte portiĝas solvita en la sango, sed la plejparto kombiniĝas kun la hemoglobino. La rilato inter Pa O2 kaj la saturiteco de hemoglobino per oksigeno estas nerekta [vd. Fig. 2].
La saturitecon per oksigeno montras la koloro de la sango; sango plena de oksigeno estas hele ruĝa. Oni povas mezuri la koloron de la sango, kaj tiel la saturitecon per oksigeno, se oni pasigas lumon tra la fingro de infano kaj mezuras la kvanton, kiu trapasas je du ondolongoj, ruĝa kaj transruĝa. La mezuro devas sinkroniĝi al la pulso, por ke ĝi rilatu al la arteria sango, ne la vejna. Estas mezurilo por tiu mezurado kiu ofte uziĝas en malsanulejoj. Estas alia mezurilo kiu rekte mezuras la metabolan staton de la cerbo. Tiu estas nuklea magneta resonanca spektromezurilo (NMR), kiu uzas 31P spektromezuradon por kalkuli la proporciojn inter kelkaj fosforaj kombinaĵoj en la cerbo. Tiu donas pli ĝustan rezulton ol la mezurado de oksigeno en la sango de la fingro. Tamen, la mezurilo funkcias malrapide; bezonante kvar minutojn por konstati la proporciojn precize ĝis 15 %. Plue, ĝi ne estas tre oportuna; la infano devus esti en magneta kampo de ĉirkaŭ 1,8 Tesla, kaj tiu bezonas superkonduktan magneton. La mezurilo estas tre altkosta, kaj ĉi-tempe troviĝas nur malmultaj en la mondo. Tamen, la regilo priskribata povos uzi tian mezurilon, se ĝi estos havebla.
La responda rapideco de la regilo tre gravas. Normala plenkreskulo tolerus mankon de oksigeno en la sango dum ĉirkaŭ kvar minutoj, antaŭ ol la cerbo difektiĝus. Normala infano, dum naskiĝo, necese estas tre tolerema al manko de oksigeno, sed eble malsana infano ne estas tiel tolerema. Ĉiuokaze, oni bezonas tempon por enmeti la infanon en la kapuĉon, do estas plej bone, ke la regilo respondu en la daŭro de ĉirkaŭ unu minuto.
Por projekti regilon, oni devas scii la dinamikon de la sistemo. Estas du efikoj, kiuj gravas. Unue, troviĝas prokrastoj. Tiuj estas, ekz. la tempo dum kiu fluas gaso tra tuboj, aŭ sango fluas tra angioj. Ni supozas ke la gasfluo estas konstanta, sed la proporcio de oksigeno varias. Se la enmeta proporcio estas u(t), kaj la elmeta proporcio estas y(t), la rilato inter ili estas
| y(t) = u(t - T) | [1] |
en kiu T estas la prokrasto kaj t la tempo. Estas simila rilato pri oksigeno en la sango, ĉar la sango bezonas tempon por flui el la pulmoj ĝis la mezurilo ĉe la fingro. La totala sistema prokrasto, Td, estas tipe dudek sekundoj. La alia grava efiko estas tempo-konstanto. Oni enmetas la infanon en kapuĉon, en kiun fluas la gaso. Pro la volumeno de la kapuĉo, oni bezonas tempon por ŝanĝi la oksigenan proporcion por la infano. La rilato inter la proporcio en la fluo, u(t), kaj la proporcio en la kapuĉo, y(t), estas
| u(t) = y(t) + Ti(dy/dt) | [2] |
Tipe, Ti estas 30 ĝis 60 sekundoj.
Per la laplace-a transformo de ekvacio [2], oni povas skribi
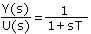 | [3] |
(Legantoj, kiuj ne konas la laplacan transformon, povas rigardi la varianton s kiel la diferencialan operatoron, d/dt. La diferenco ne gravas por la nuna desegno. La konstanta stata valoro de la elmeto, por enmeto de unu unuo, estas la valoro de la esprimo en [3] por s = 0, aŭ la limo, kiam s proksimiĝas al 0.) La esprimo en ekvacio [3] nomiĝas la transigfunkcio (TF).
Troviĝas ankaŭ tempo-konstanto por la funkcio de la pulmoj. Tipe ĝi estas dek sekundoj. La TF el FeO2, la oksigena proporcio en la fluo, ĝis PaO2 estas
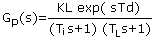 | [4] |
La parametro KL estas la konstante stata valoro de tiu TF. Ĝi varias kun la sanstato de la infano, kaj tiu estas grava problemo por la regilo. La eksponenciala termo estas la laplaca transformo de la prokrasto.
Pro kelkaj kialoj, estas necese, ke komputoro uziĝu por la regilo. Oni povas figuri la tutan sistemon, inklude la regilon, per Fig. 3.
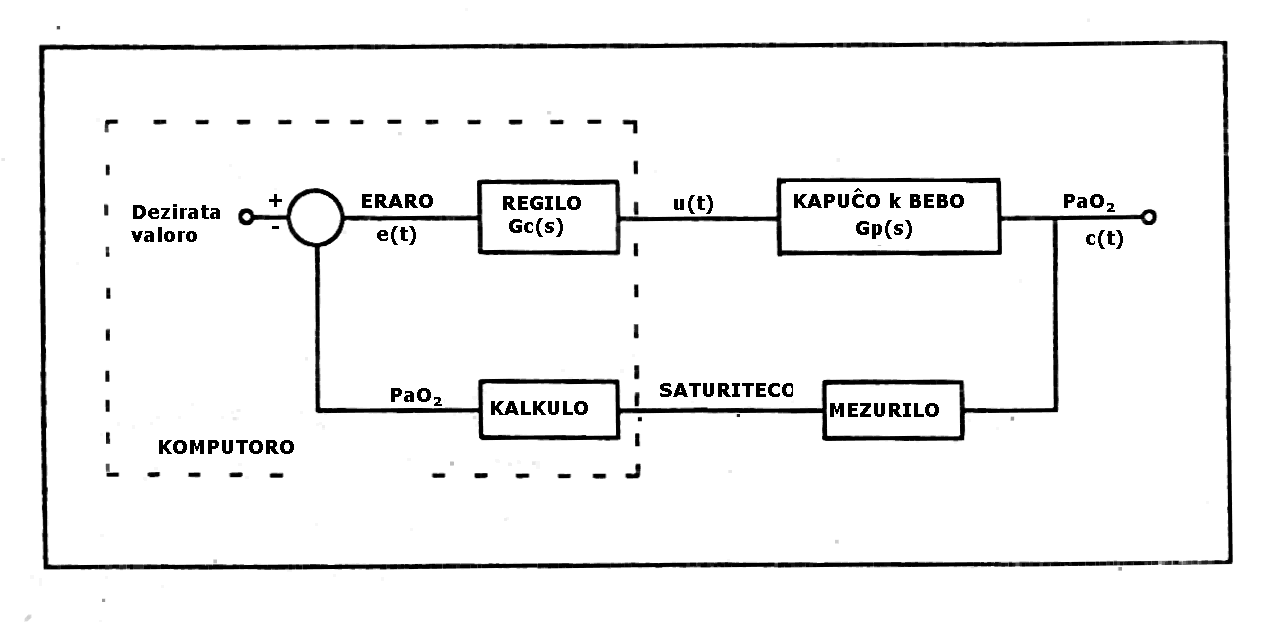
Fig. 3: Bloka figuro de la sistemo
La elmeto de la mezurilo estas la valoro de saturiteco per oksigeno, kiu nerekte rilatas al Pa O2. Por bone regi la sistemon, necesas, ke la nerekteco nuliĝu. Tion povas fari la komputoro, kiu kalkulas Pa O2 el la mezuro de saturiteco per oksigeno. 'Erara' signalo, e, kalkuliĝas kiel la diferenco inter la dezirata valoro de Pa O2 kaj la valoro el la mezuro.
La elektita formo de regilo estis la t.n. "triterma regilo". En tiu, adiciiĝas la eraro, la diferencialo de la eraro, kaj la integralo de la eraro, en taŭgaj proporcioj. La TF de la regilo estas
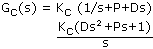 | [5] |
en kiu Kc, P kaj D estas konstantoj. P kaj D elektiĝas por nuligi la tempajn konstantojn en ekvacio [4], kaj pro tio
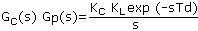 | [6] |
(Fakte la signaloj en la komputoro ne estas kontinuaj, sed estas specimenataj ĉe intervaloj de dek sekundoj. Por la analizo oni bezonas la z-transformon. Por tiu desegno, la kompliko ne necesas.)
La esprimo de ekvacio [6] estas la TF el e ĝis c. Skribante G(s) por Gc (s) Gp (s), kaj K por Kc KL, ni havas
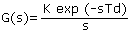 | [7] |
Kiam s proksimiĝas al nulo, G(s) senlime pligrandiĝas. Tio signifas, ke, en la konstanta stato, la erara signalo, e, iĝas nulo, kaj r precize egalas c. La signalo u ne estas nulo. Tiu rezultas de la integrala termo en la regilo. Por rapida respondo, K devus esti tiom granda kiom eble, sed se ĝi estus tro granda, la sistemo estus nestabila. Per ekvacio [7] kaj la rilato e = r - c, oni povas kalkuli ke la TF el r ĝis c estas
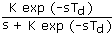 | [8] |
La ŝlosilo al stabileco estas la karakteriza ekvacio,
| s + K exp (-sTd) | [9] |
Kiam s proksimiĝas al la radikoj de [9], la esprimo [8] senlime pligrandiĝas. Ekvacio [9] havas infinitan nombron da kompleksaj radikoj. Estas pruveble, ke, se la reala parto de ĉiu radiko de karakteriza ekvacio estas malpli ol nulo, la sistemo estas stabila. Por ekvacio [9] tio okazas se, kaj nur se validas
| 0 < K < π/2Td | [10] |
Se K proksimiĝus al π/2Td, eĉ se malpli, la sistemo elmontrus malmulte dampitajn osciladojn. Por sufiĉe dampita, sed kiom eble rapida respondo, duono de tiu valoro taŭgas.
Kelkaj parametroj, kiuj gravas por la regilo, povas varii. Tj kaj Td povas sufiĉe precize taksiĝi, kaj oni povas enmeti la valorojn en la komputoron. Pri Ti oni ne certe scias, kaj bezonas pluan esploradon. Eble la variado estos tiom sufiĉe malgranda, kiom ne gravas por la regado. La variado en KL tre gravas. Por normala infano, la valoro estas kvinoble de tiu por tre malsana infano. Se oni elektus Kc por bona respondo por normala infano, la respondo por malsana infano estus tre malrapida; aliflanke, se oni elektus Kc por malsana infano, la sistemo estus nestabila por normala infano. Dum la kuracado efikas, malsana infano iom post iom saniĝas, kaj KL pligrandiĝas, kaj, por bona rego, Kc devas akomodiĝi. Se la kuracisto, per sia profesia scipovo, taksus la unuan oksigenan bezonon de la infano, la komputora programo pro tio povus kalkuli unuan valoron de KL kaj, se necesus, TL. Pro tiuj valoroj, la programo kalkulus taŭgajn parametrojn por la regilo. Post tio, la programo devus konstati novajn valorojn por KL kaj, se necesus, TL.
Estas kelkaj rimedoj por tio (ÅSTRÖM-WITTENMARK 1984). La metodo de minimumaj kvadratoj ŝajnas alloga; oni devas registri, dum sufiĉe longa tempo, la enmeton kaj elmeton de sistemo (u kaj c en Fig. 3). Tiam oni kalkulas la parametrojn de matematika modelo kiu, kun enmeto u, havas elmeton, kiu plej bone proksimiĝas al c. La metodo trovas la modelon, kiu havas minimuman sumon de kvadratoj de eraroj. Tamen, se la enmeto ne taŭgas por malkovri la parametrojn, la kalkulado povas liveri tute malĝustajn rezultatojn, do la metodo havas danĝerojn por aŭtomata rego. Se oni bezonas trakti nur KL kaj ne TL, estas tre simpla metodo, kiu eblas, ĉar la sistemo, dum la plejparto de la tempo, estas proksimume en konstanta stato. Kiam la sistemo ŝanĝiĝas nur malrapide, la programo kalkulas, el la rezultoj de mezurado, Pa O2/FcO2, kaj iomete ŝanĝas KL cele al tiu valoro. Tiam kalkuliĝas novaj parametroj por la regilo.
Figuro 4 montras unu rezulton de komputora ŝajnigado de la sistemo kun malsana infano.
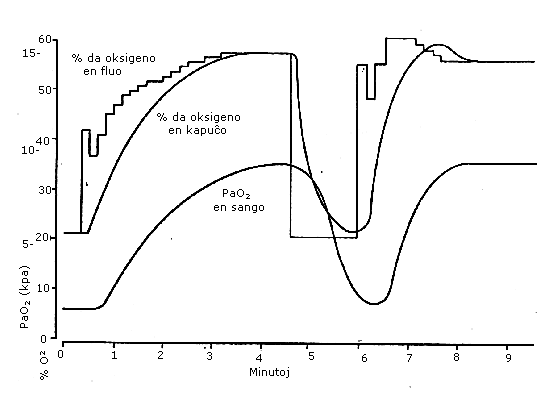
Fig. 4: Komputora ŝajnigado
La infano bezonis 58 % da oksigeno en la aero por subteni normalan oksigenan nivelon en la sango. Tamen, la cifero enmetita en la programon estis 21 %, do la unua valoro de Kc estis tro malgranda. Unue, la infano estis enspirinta aeron kun 21 % da oksigeno. 20 sekundojn post la komenciĝo de la registrado, la aŭtomata regilo estis funkciigata. Post dek sekundoj (la prokrasto por la aero), la oksigeno en la kapuĉo plialtiĝis, kaj post pluaj dek sekundoj (la prokrasto por la sango), plialtiĝis la oksigeno ensanga. La respondo estis malrapida kaj tro dampita; ĝi bezonis du minutojn, plus la prokraston, por ke la ensanga oksigeno atingu sendanĝeran nivelon. Post kvar minutoj kaj duono, kiam la niveloj estis konstantaj, la regilo malŝaltiĝis, kaj la infano enspiris 21 % da oksigeno dum naŭdek sekundoj. Aŭtomata rego denove estis funkciigata, kaj, ĉi-foje, pro la memakomodo, la respondo estis pli rapida; ĝi bezonis malpli ol unu minuton por atingi sendanĝeran nivelon.
| c | elmeta signalo de rega sistemo |
| e | 'erara' signalo de rega sistemo |
| FcO2 | proporcio de oksigeno en la fluo de aero |
| FiO2 | proporcio de oksigeno en enspirata aero |
| Gc(s) | transigfunkcio de regilo |
| Gp(s) | transigfunkcio el FcO2 ĝis PaO2 |
| KL | konstante stata valoro de PaO2/FiO2 |
| PaO2 | parta premo de oksigeno en la sango, kPa |
| r | dezirata elmeta signalo en rega sistemo |
| t | tempo |
| Td | prokrasto de la sistemo |
| Ti | tempo-konstanto de la kapuĉo |
| TL | tempo-konstanto de la pulmoj |
| u(t) | enmeta signalo |
| U(s) | laplaca transformo de u(t) |
| w | frekvenco, radianoj en unu sekundo |
| y(t) | elmeta signalo |
La verkisto, kiu laboris kun Phospho-Energetics, Usono, dum 1986, esprimas dankon pro la permeso de Phospho-Energetics, por publikigi la enhavon de tiu verko. La esploradon subvenciis la usona Nacia Instituto de Sano, subvencio IR43, 22309-01, Phospho-Energetics.
Automatic Control of Oxygen Flow for Neonates -- (anglalingva resumo)
This paper discusses the design of an automatic oxygen controller for newborn babies under incubator treatment. A three term controller is suitable, but, because of parameter changes, adaptive control is required. Results from a computer simulation are shown.
| Fonto: Scienca Revuo, Vol. 39 (1988) - 155, pĝ. 43-52. | STEB: http://www.eventoj.hu/steb/ |