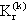 , la kompleta k-grafiko de ordo r.
, la kompleta k-grafiko de ordo r.k-grafiko aŭ k-uniforma hipergrafiko G estas paro (V,E), kie V = V(G) estas aro kaj E = E(G) estas familio de k-elementaj subaroj de V. n = n(G) := |V| estas la ordo de G, dum e = e(G) := |E| estas ĝia grando. La elementoj de V nomiĝas verticoj kaj la elementoj de E k-eĝoj aŭ, mallonge, eĝoj de G. Por aro S ⊂ V ni difinas la gradon d(S) kiel la nombron de la eĝoj entenantaj S. G1 nomiĝas subgrafiko de G2, se V(G1) ⊂ V(G2) kaj E(G1) ⊂ E(G2).
Tiu k-grafiko G kun ordo r, por kiu ĉiu k-elementa subaro de V(G) estas elemento de E(G), nomiĝas 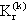 , la kompleta k-grafiko de ordo r.
, la kompleta k-grafiko de ordo r.
P. TURÁN [1] demandis pri la valoroj de la funkcio ex(n,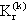 ), difinita kiel la maksimuma grando de k-grafiko de ordo n entenanta neniun
), difinita kiel la maksimuma grando de k-grafiko de ordo n entenanta neniun 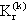 .
.
Li konjektis, ke se m := (r–1) / (k–1) estas entjera, tiam la sekva konstruo liveras ekstreman k-grafikon, t.e. k-grafikon de ordo n kaj grando ex(n,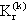 ), kiu entenas neniun
), kiu entenas neniun 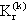 : Dividu n verticojn en m disajn klasojn, kiuj estu tiel egale grandaj kiel eblas, kaj prenu kiel eĝojn ĉiujn arojn de k verticoj, kiuj ne ĉiuj troviĝas en la sama klaso.
: Dividu n verticojn en m disajn klasojn, kiuj estu tiel egale grandaj kiel eblas, kaj prenu kiel eĝojn ĉiujn arojn de k verticoj, kiuj ne ĉiuj troviĝas en la sama klaso.
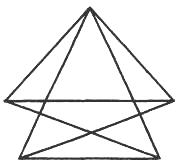
Fig. 1
Ni nomas la ĵus konstruitan k-grafikon 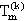 (n); Fig. 1 montras la 2-grafikon
(n); Fig. 1 montras la 2-grafikon 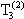 (5). Se ni nomas la aron de la ekstremaj k-grafikoj EX(n,
(5). Se ni nomas la aron de la ekstremaj k-grafikoj EX(n, 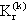 ), ni povas formuli la konjekton de TURÁN jene:
), ni povas formuli la konjekton de TURÁN jene:
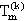 (n) ⊂ EX(n,
(n) ⊂ EX(n, 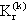 ) por ĉiuj entjeraj k≥2, m≥2 kun m = (r-1)/k-1).
) por ĉiuj entjeraj k≥2, m≥2 kun m = (r-1)/k-1).
TURÁN pruvis sian konjekton por k = 2. Ni montras, ke en la kazo r < k2 -3k+3 ĝi estas malĝusta por ĉiu sufiĉe granda n. Tiucele ni unue konstatas, ke ĉiu ekstrema k-grafiko G ⊂ EX(n, 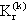 ) devas plenumi la sekvan kondiĉon:
) devas plenumi la sekvan kondiĉon:
(*) d(S) ≥ ex(n-k-f 2, 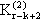 ) por ĉiu (k-2)-elementa aro S ⊂ V(G).
) por ĉiu (k-2)-elementa aro S ⊂ V(G).
Se tiu ĉi kondiĉo ne estus plenumita, ni povus plialtigi la grandon de G sen ke estiĝas iu 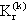 : Konstruu sur la verticaro V(G)-S iun ekstreman H ∈ EX(n-k+2,
: Konstruu sur la verticaro V(G)-S iun ekstreman H ∈ EX(n-k+2, 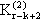 ). Forigu de G ĉiujn k-eĝojn entenantajn S kiel subaron kaj aldonu kiel novajn k-eĝojn ĉiujn uniojn de S kun unu el la ex(n-k+2,
). Forigu de G ĉiujn k-eĝojn entenantajn S kiel subaron kaj aldonu kiel novajn k-eĝojn ĉiujn uniojn de S kun unu el la ex(n-k+2, 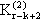 ) 2-eĝoj de H. Ni tiam ricevas k-grafikon G' kun grando:
) 2-eĝoj de H. Ni tiam ricevas k-grafikon G' kun grando:
e(G') = e(G) - d(S) + ex(n-k+2, 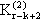 ) > e(G).
) > e(G).
Laŭ nia konstruo ankaŭ G' entenas neniun 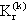 kiel subgrafikon, ĉar ties verticaro rajtus nek enteni nek ne enteni S kiel subaron. Sekve G ne estis ekstrema. Ni do ricevas kontraŭdiron.
kiel subgrafikon, ĉar ties verticaro rajtus nek enteni nek ne enteni S kiel subaron. Sekve G ne estis ekstrema. Ni do ricevas kontraŭdiron.
Ĉar la konjekto de TURÁN estas ĝusta por k=2, ni povas determini la valoron de ex(n-k+2, 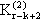 ). La probablo, ke iu paro el n-k+2 verticoj ne estas eĝo de fiksita 2-grafiko
). La probablo, ke iu paro el n-k+2 verticoj ne estas eĝo de fiksita 2-grafiko 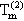 (n-k+2) kun m=r-k+l konverĝas por n→∞ al 1/m=1/(r-k+1); sekve ex(n-k+2,
(n-k+2) kun m=r-k+l konverĝas por n→∞ al 1/m=1/(r-k+1); sekve ex(n-k+2, 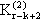 ) = (1 -1 / (r-k+1)) (
) = (1 -1 / (r-k+1)) (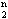 ) + o(n2), kie o(n2) estas funkcio, kiu dividite per n2 konverĝas al 0 por n→∞.
) + o(n2), kie o(n2) estas funkcio, kiu dividite per n2 konverĝas al 0 por n→∞.
El (*) do sekvas
(**) d(S) ≤ (1 - 1 / (r - k + 1)) (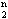 ) + o(n2).
) + o(n2).
Ni nun montras, ke por r < k2 - 3k + 3 la k-grafiko 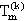 (n) ne ĉiam plenumas tiun ĉi kondiĉon: Se S konsistas el k – 2 verticoj el nur unu vertica klaso de la
(n) ne ĉiam plenumas tiun ĉi kondiĉon: Se S konsistas el k – 2 verticoj el nur unu vertica klaso de la 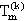 (n), tiam
(n), tiam
(***) d(S) = (1 – 1 / m2) (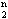 ) + o(n2),
) + o(n2),
ĉar por paro de du pliaj verticoj el V(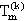 (n)) la probablo, ke ili ambaŭ troviĝas en la sama vertica klaso kiel S [kaj ne formas kune kun S eĝon de la
(n)) la probablo, ke ili ambaŭ troviĝas en la sama vertica klaso kiel S [kaj ne formas kune kun S eĝon de la 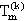 (n)], konverĝas por n→∞ al 1 / m2.
(n)], konverĝas por n→∞ al 1 / m2.
El nia premiso r < k2–3k+3 kaj la difino m := (r–1) / (k–1) sekvas:
r–1 <(k–1) (k–2) kaj do m<k–2,
sekve r–k+1 = m(k–1)+1–k+1 = (m–1) (k–1)+1<(m–1)(m+1)+1= m2
kaj do 1 – 1 / (r–k+1) < 1 – 1 / m2.
Pro tio (**) kontraŭdiras al (***), se n estas sufiĉe granda, kaj ni pruvis:
Teoremo. Por ĉiu paro (k,r) kun 3 ≤ k < r < k2–3k+3 ekzistas N(k,r) tiel, ke por ĉiu n ≤ N(k,r) la konjekto de TURÁN estas malĝusta.
[1] P. TURÁN: Applications of graph theory to geometry and potential theory, en Combinatorial structures and their applications (R. Guy k.a. eld.), Gordon and Breach, New York 1970.
| Fonto: Scienca Revuo Vol. 45 (1994)(2)-165. pp. 26-30. | STEB: http://www.eventoj.hu/ |